Mathematical Modeling
Phase Dynamics
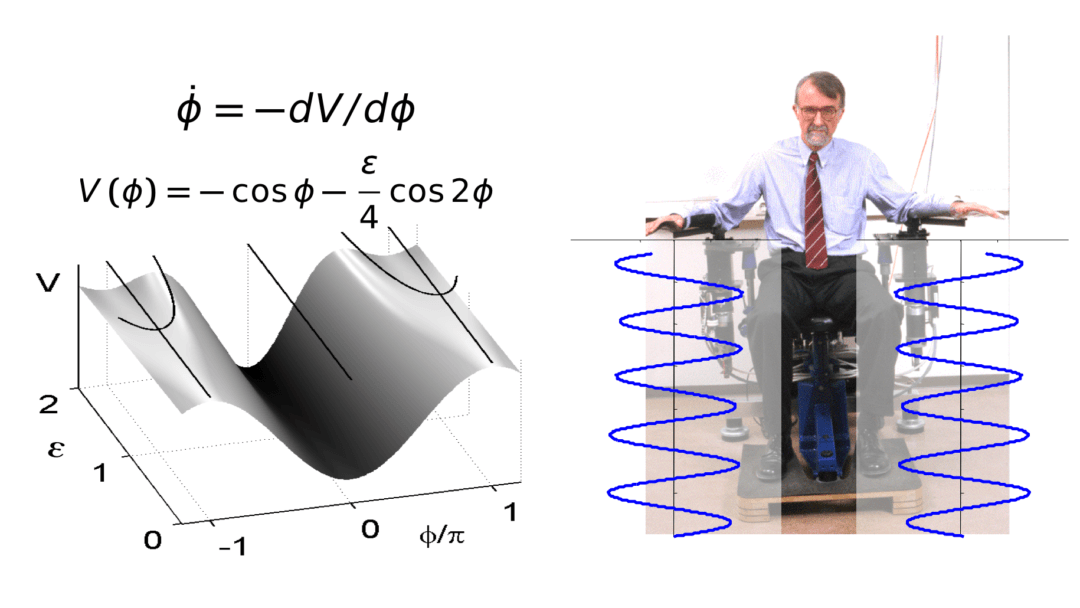
Relative Phase Dynamics
The stability of coordination can often be addressed via the relative phase between the individual limb movements. We are studying in detail the effect of different interactions between limbs, effects of noise and non-autonomous forcing.
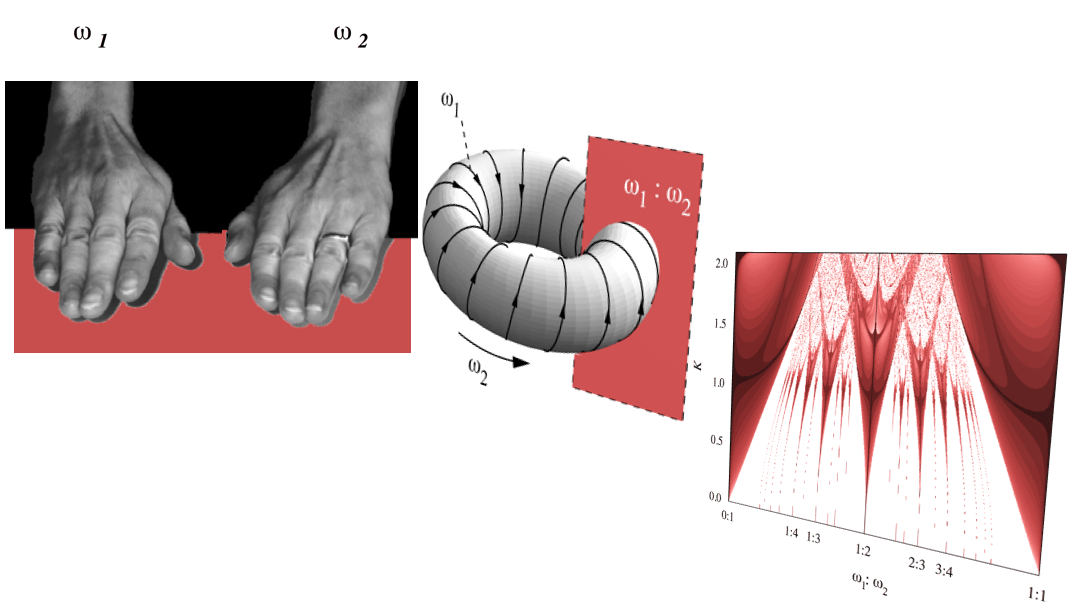
Bimanual Coordination
We study how different control processes contribute to stabilizing the coordination between limbs, and how they change as a function of, e.g., movement frequency and amplitude, learning, development and pathology.
Networks of Non-Linear Oscillators
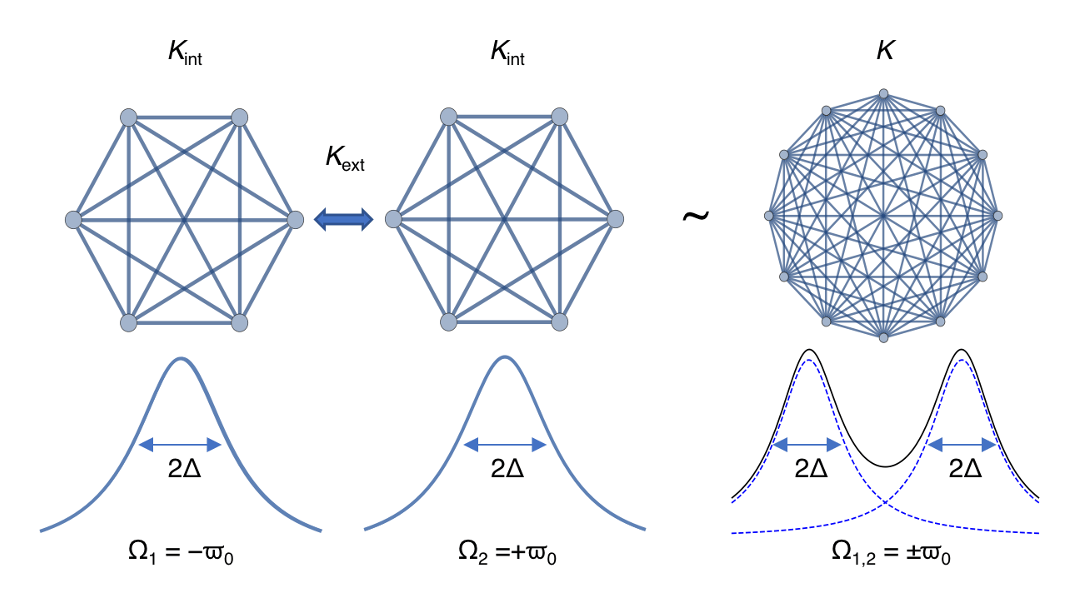
Network-Network Interactions
We analyze cross-frequency synchronizability of complex, functional networks accompanying different oscillatory regimes with focus on effects of mutual transfer of network structures, e.g., via the type of clustering or the correlations of random components.

COSMOS
Complex Oscillatory Systems: Modeling and Analysis. In this EU-funded Marie Skłodowska Curie ITN, 15 ESRs are being trained in nonlinear dynamics, numerical methods, statistical mechanics and, where needed, basics of neuroscience, physiology, and system biology.
System Identification
Information about this topic will be available soon